在本出版物中,我们将考虑什么是高斯方法,为什么需要它,以及它的原理是什么。 我们还将使用一个实际示例演示如何应用该方法来求解线性方程组。
内容
高斯方法的描述
高斯法 是用于求解的经典变量顺序消除方法。 它以德国数学家卡尔·弗里德里希·高斯(Carl Friedrich Gauss,1777-1885)的名字命名。
但首先,让我们回顾一下 SLAU 可以:
- 有一个单一的解决方案;
- 有无数个解;
- 不兼容,即没有解决方案。
实际好处
高斯方法是求解包含三个以上线性方程以及非方形系统的 SLAE 的好方法。
高斯方法的原理
该方法包括以下步骤:
- 直 – 对应于方程组的增广矩阵通过行上方的方式减少为上三角(阶梯式)形式,即在主对角线下方应该只有等于零的元素。
- 背部 – 在生成的矩阵中,主对角线上方的元素也设置为零(下三角视图)。
SLAE 解决方案示例
让我们使用高斯方法求解下面的线性方程组。
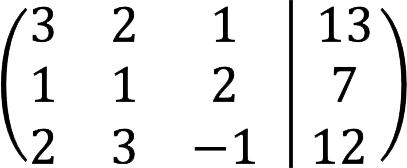
解决方案
1. 首先,我们以扩展矩阵的形式呈现 SLAE。
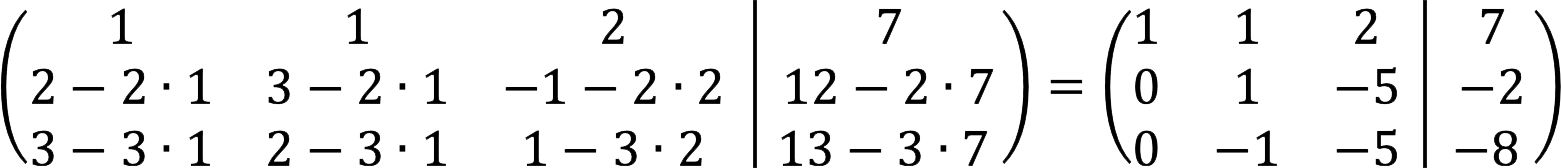
2. 现在我们的任务是重置主对角线下的所有元素。 进一步的行动取决于具体的矩阵,下面我们将描述适用于我们案例的那些。 首先,我们交换行,从而将它们的第一个元素按升序排列。
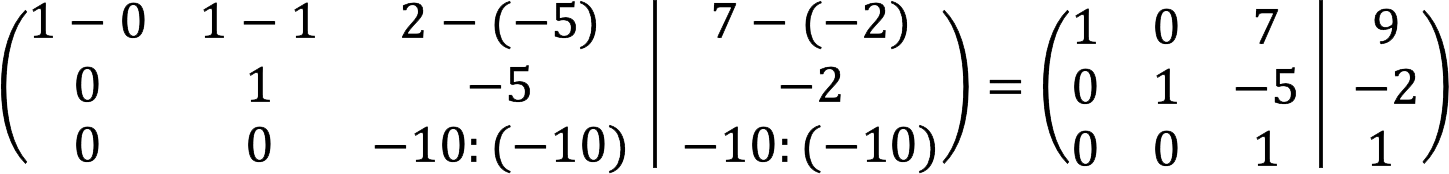
3. 第二行减去第一行的两倍,第三行减去第一行的三倍。
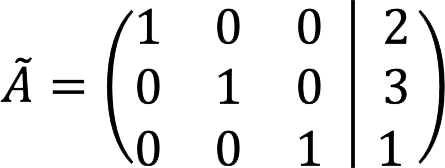
4.将第二行添加到第三行。
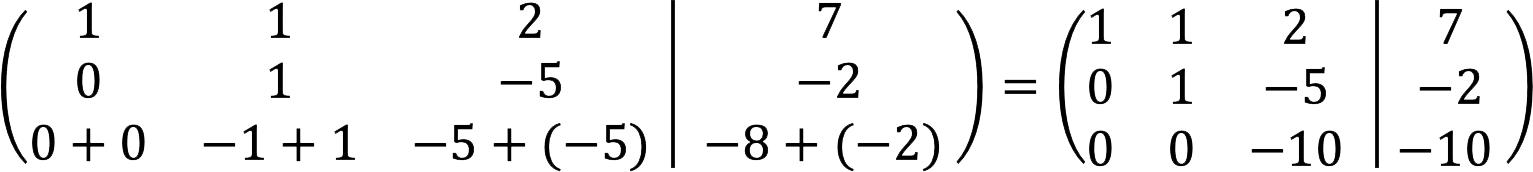
5. 第一行减去第二行,同时将第三行除以-10。
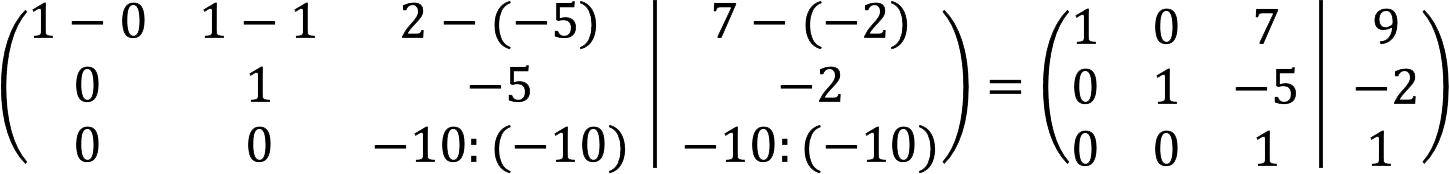
6.第一阶段完成。 现在我们需要获取主对角线上方的空元素。 为此,请从第一行中减去乘以 7 的第三行,然后将乘以 5 的第三行与第二行相加。
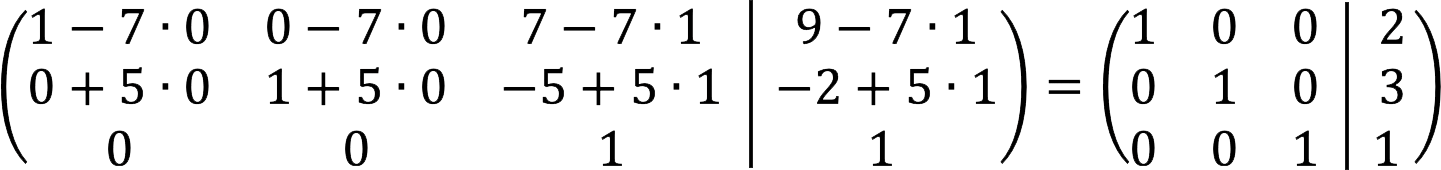
7. 最终展开的矩阵如下所示:
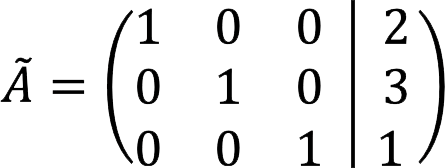
8. 它对应于方程组:
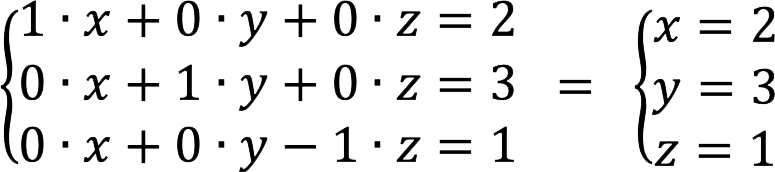
答: 根 SLAU: x = 2, y = 3, z = 1。










