在本出版物中,我们将考虑矩阵秩的定义以及可以找到它的方法。 我们还将分析示例以展示理论在实践中的应用。
确定矩阵的秩
矩阵秩 是其行或列系统的等级。 任何矩阵都有其行秩和列秩,它们彼此相等。
行系统等级 是线性独立行的最大数量。 列系统的排名以类似的方式确定。
笔记:
- 零矩阵的秩(用符号“θ") 任何大小都是零。
- 任何非零行向量或列向量的秩都等于 XNUMX。
- 如果任意大小的矩阵包含至少一个不等于 XNUMX 的元素,则其秩不小于 XNUMX。
- 一个矩阵的秩不大于它的最小维数。
- 对矩阵执行的基本变换不会改变其秩。
求矩阵的秩
边缘小方法
一个矩阵的秩等于一个非零的最大阶数。
算法如下: 从最低的顺序到最高的顺序找到未成年人。 如果轻微 nth 阶不等于 XNUMX,并且所有后续 (n + 1) 等于 0,所以矩阵的秩是 n.
例如:
为了更清楚,我们举一个实际的例子,求矩阵的秩 A 下面,采用接壤未成年人的方法。
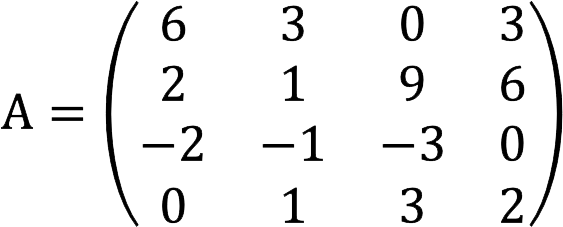
解决方案
我们正在处理一个 4 × 4 的矩阵,因此它的秩不能高于 4。此外,矩阵中有非零元素,这意味着它的秩不小于 XNUMX。 那么让我们开始吧:
1.开始检查 二级未成年人. 首先,我们取第一列和第二列的两行。
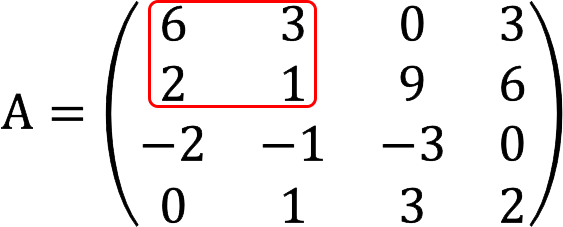
次要等于零。
![]()
因此,我们继续下一个小调(第一列保留,而不是第二列,我们取第三列)。
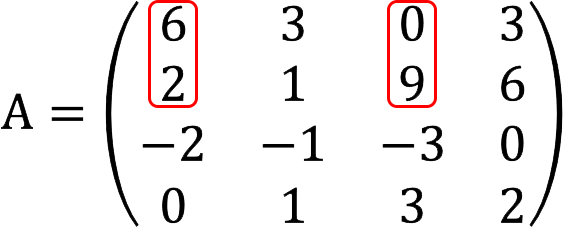
次要是54≠0,所以矩阵的秩至少是XNUMX。
![]()
请注意: 如果这个次要结果等于 XNUMX,我们将进一步检查以下组合:
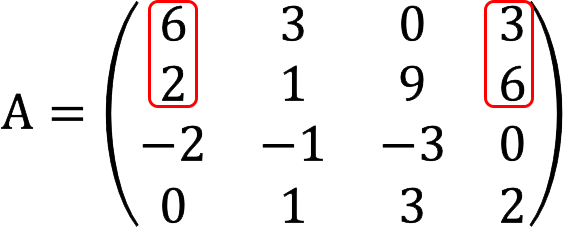
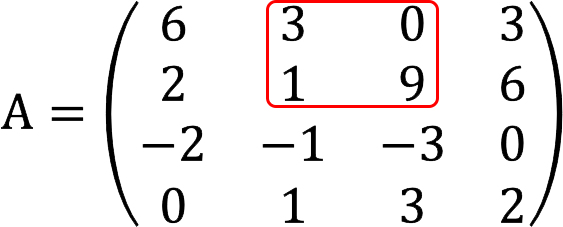
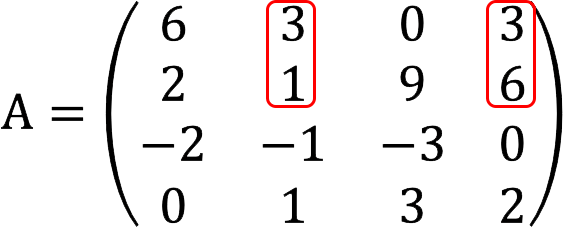
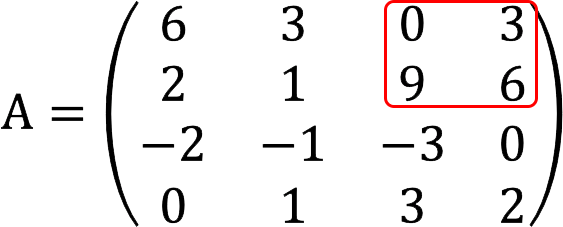
如果需要,可以使用字符串以相同的方式继续枚举:
- 1和3;
- 1和4;
- 2和3;
- 2和4;
- 3和4。
如果所有二阶小数都等于 XNUMX,那么矩阵的秩就等于 XNUMX。
2. 我们几乎立刻就找到了适合我们的未成年人。 所以让我们继续 三阶未成年人.
对于得到非零结果的二阶次要,我们添加一行和一列以绿色突出显示(我们从第二个开始)。
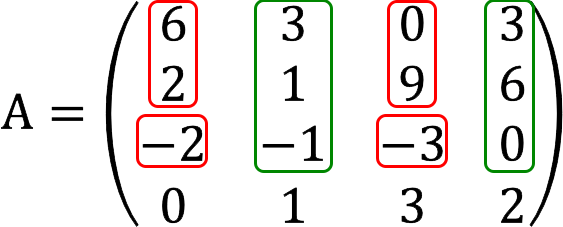
未成年人原来是零。
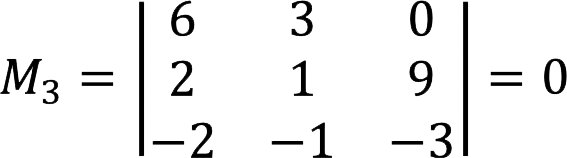
因此,我们将第二列改为第四列。 在第二次尝试中,我们设法找到了一个不等于 3 的小数,这意味着矩阵的秩不能小于 XNUMX。
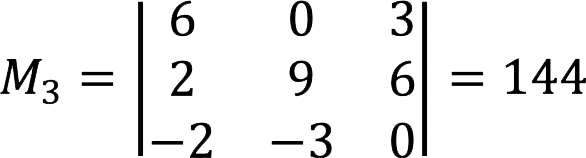
请注意: 如果结果再次为零,而不是第二行,我们将继续第四行并继续搜索“好”未成年人。
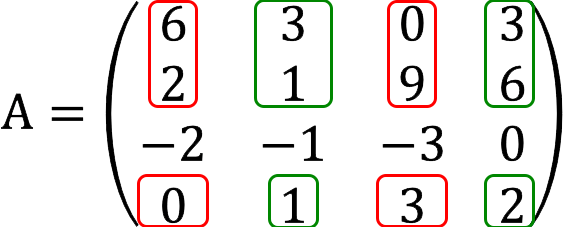
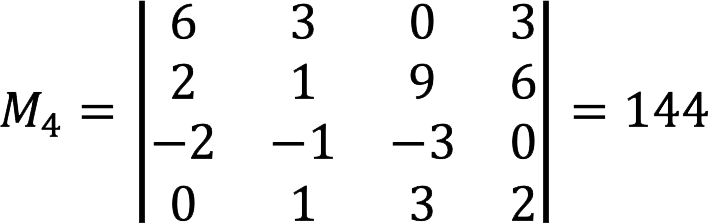
3. 现在还有待确定 四阶未成年人 根据之前的发现。 在这种情况下,它与矩阵的行列式匹配。
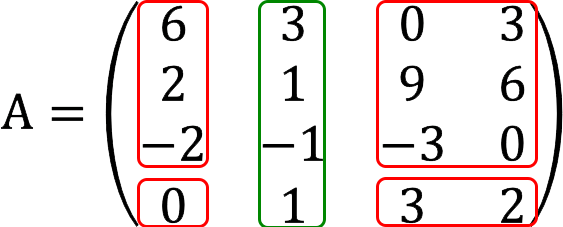
次要等于 144≠0。 这意味着矩阵的秩 A 等于4。
将矩阵简化为阶梯形式
一个阶跃矩阵的秩等于它的非零行数。 也就是说,我们需要做的就是将矩阵带入适当的形式,例如,使用 ,正如我们上面提到的那样,它不会改变它的等级。
例如:
求矩阵的秩 B 以下。 我们不举一个过于复杂的例子,因为我们的主要目标只是演示该方法在实践中的应用。
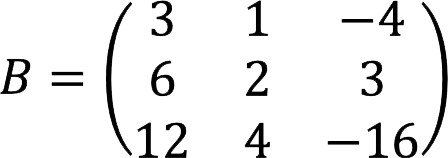
解决方案
1.首先,从第二行中减去加倍的第一个。
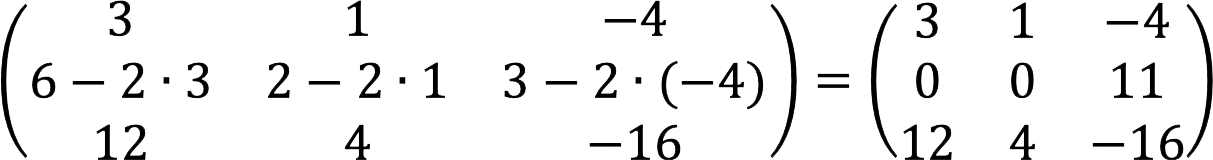
2. 现在从第三行减去第一行,乘以四。
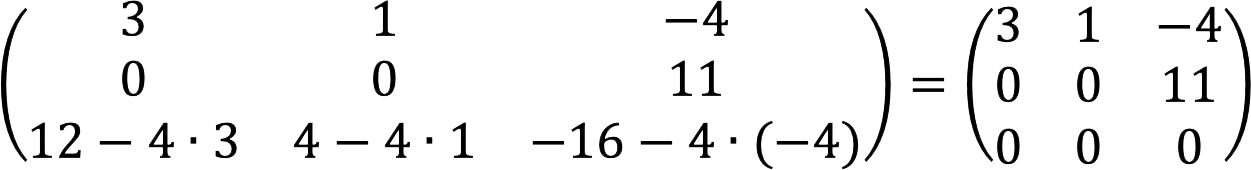
因此,我们得到了一个步进矩阵,其中非零行数等于 2,因此它的秩也等于 XNUMX。










